Quantum Model
Clueless Cat: OmniSCIENTIST Onion, What are you looking at?
Onion the Omniscientist: Well Clueless Cat, it's a picture of the best atomic model based on current scientific data, which is now called the Quantum Model.
Clueless Cat: Umm... What is the Quantum Model?
Onion the Omniscientist: Well, to start off, the Heinsenberg Uncertainty Principle, stating that the position and velocity of an electron (or any other particle) can not be determined simultaneously, is the foundation for the Quantum Model. Although there is always an uncertainty in locating electrons, in the Quantum Model, it states that you can determine the probability where electrons may be found in certain (3-D) regions around the nucleus in an atom, called orbitals.
Clueless Cat: Other than these orbitals, is that all that makes up the Quantum Model? I thought that an atom is made up of protons and neutrons as well.
Onion the Omniscientist: Ah, that's right! There's more than just the orbitals which you can see here, because it evolved from many earlier models of the atom. Those earlier models, based upon experiments, supported the inferences of different parts of the atom, such as the nucleus. If you want more information on a couple of the earlier models, go to any of the links at the top of the page.
Clueless Cat: Aah... But what is the nucleus?
Onion the Omniscientist: It's a small, dense part at the center of the atom made up of exactly what you mentioned, protons and the neutrons.
Clueless Cat: Wow! So atoms aren't fundamental; they can be broken down into smaller pieces! May you also inform me what's the difference between these two types of particles?
Onion the Omniscientist: To start with the basics, protons are positively charged and neutrons have a neutral charge. Another type of particle that surrounds the nucleus, called electrons, are negatively charged. Unlike protons and neutrons, electrons are not found in a specific location of the atom. They are the particles that make up the orbitals in the Quantum Model.
Clueless Cat: I’m very interested in these “orbitals.” Can you tell me more about them?
Onion the Omniscientist: Sure! The Schrödinger Wave Equation described orbitals, which are three-dimensional, and therefore it required three coordinates or the first three quantum numbers. Quantum numbers describe the properties of the orbitals and the electrons.
Clueless Cat: Wait... What is the Schrödinger Wave Equation?
Onion the Omniscientist: Based on experiments that resulted in the dual wave-particle nature of light, Schrödinger hypothesized that electrons, a matter which was revealed to be related to light, also had this nature for his Wave Equation. The solutions to his equation are called wave functions, which only give the probability of locating an electron around the nucleus. But anyways, the first three quantum numbers that resulted from the Schrödinger Wave Equation are the principal (n), angular momentum (l), and the magnetic quantum numbers (m).
Clueless Cat: What do these quantum numbers have to do with the orbitals?
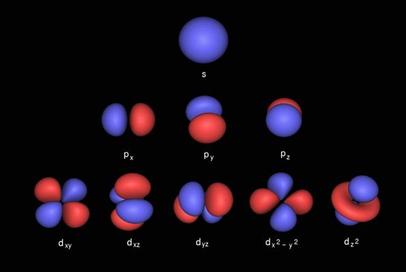
Onion the Omniscientist: The principal quantum number describes the main energy level, also know as the electron shell. When n increases, so does its average distance and the required amount of energy. The total number of possible orbitals in a shell is equal to n^2. That number comes from the total number of possible orbitals shapes, also known as subshells, which are described by the angular momentum quantum number. The possible number of subshells is equal to n of the electron shell, ranging from 0 to n-1. In the first subshells when l=0, there is only one possible orbital shape that is best described as spherical. In the second subshells when l=1, it has a polar shape. In the third subshells when l=2, it has a four-leaf-clover shape.
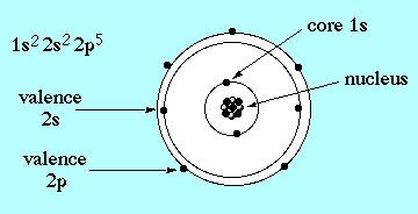
There are letters that are designated to each of the subshells; these letters s, p, and d are designated to subshells 0, 1, 2 respectively. There are more subshells but another important subshell that is too complex for me to describe is the f subshell, when l=4. The next one, the Magnetic quantum number describes how the orbitals are located around the nucleus. Since the s orbital resembles a sphere, it has only one possible orientation centered around the nucleus where m=0. Each s subshell contains only one s orbital. The p orbitals have three possible orientations because they can lie on the x, y, or z axes, which means that there are three p orbitals, px, py, and pz, in each p subshell. They can be designated with these numbers m=-1, 0, and +1, in no particular order. The possible number of orbitals in a subshell can be the integers between –l and +l. For example, the d subshells have 5 d orbitals and they correspond to the values m=-2, -1, m=0, m=+1, and m=+2. (Note: The diagram shown below is not defining the electrons in an orbit (Rutherford-Bohr Model), but that the electrons can be located anywhere in their corresponding orbitals, shown as rings.)
Clueless Cat: WOWWWWW!!!!!!!! I thought this was going to be easy! Wait, what else is there to describe about the orbitals?
Onion the Omniscientist: No, we’re done talking about orbitals! Now we’re talking about electrons! One inference based on experiments is that an orbital can hold only two electrons, each with opposite spins. The final quantum number distinguishes which electron in the orbital is being identified. It is also known as the spin quantum number because they can spin in a direction described with only these two numbers, +½ and -½.
Clueless Cat: Surprisingly, I understand what you said about the Quantum Model! In the Quantum Model, there are four quantum numbers used to name each electron in an orbital surrounding the nucleus, which is made up of protons and neutrons!
Onion the Omniscientist: Now you have the most recent picture of the atom! Since you know about this model, the other ones shouldn't be as hard to understand, so go check them out!
